Omkredsen vil altid være lige, fordi længden ganges med 2, hvilket gør den lige, og lægges til bredden, der er blevet ganget med 2, hvilket også gør den også selvom. Men hvis både længden og bredden er ulige, vil området være ulige, hvilket betyder, at det er umuligt for omkredsen at være den samme som arealet.
Kan former have samme areal og omkreds?
En todimensionel ensartet form (eller perfekt form) er en, hvis areal er numerisk lig dens omkreds. For eksempel har en retvinklet trekant med siderne 5, 12 og 13 både areal og omkreds en numerisk værdi uden enhed på 30.
Vil en firkant altid have samme areal og omkreds?
Enhver rektangel vil altid have flere af disse blokke eksponeret til ydersiden end en firkant af det samme område. Dette beviser, at et rektangel altid vil have en større omkreds end et kvadrat med samme areal. Dette indebærer, at hvis et rektangel og et kvadrat har samme omkreds, skal rektanglet have et mindre areal.
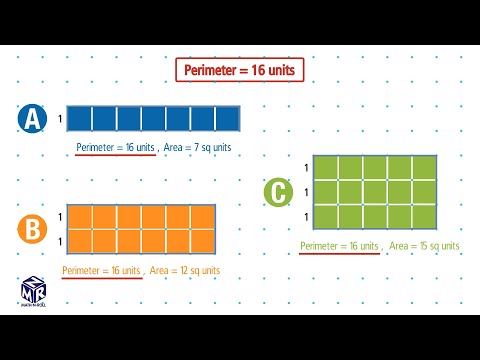
Kan omkredsen være mindre end arealet?
Omkredsen er altid større undtagen én (form G). … Arealet og omkredsen er det samme. Det samme skete, hvis du der har et rektangel, der har en længde på 6 og en bredde på 3. Tabel 3 (de gav ikke deres skole) kiggede på at finde en form, som har en omkreds numerisk to gange arealet.
Øger omkredsen med arealet?
Hvis du starter med en retlinet form, når du øger arealet, vil omkredsen øges.